$1.\int{\frac{1}{\sqrt{x^2±a^2}}}dx=ln|x+\sqrt{x^2+a^2}|+C(a>0)$ $1.5.特别地, \int{\frac{1}{\sqrt{x(x+a)}}}dx=ln(\sqrt{x}+\sqrt{x+a})+C(a>0)$ $2.\int{tan^2(x)}dx=tanx-x+C$ $3.\int{\frac{1}{x^2+a^2}}dx=\frac{arctan{(\frac{x}{a})}}{a}+C$ $4.\int{\fra……

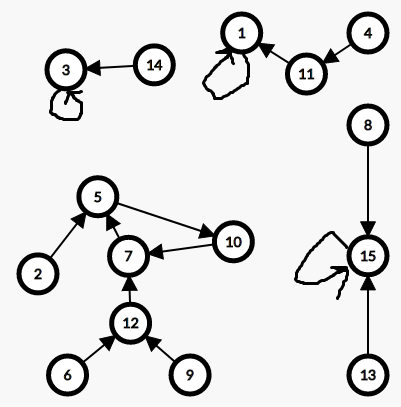
OGF - Cayley Formula Question Statement Prove # of trees on [n] = n^{n-2} Solution f:(1,2,3,...,n)\to(1,2,3,...,n) f(1)=1,f(n)=n Functional Digraph(directed graph) D V(D)=[n] 编者注：V为节点集合 (i,j)\in E(D) if f(i)=j 注：E为边集合 Example | ……

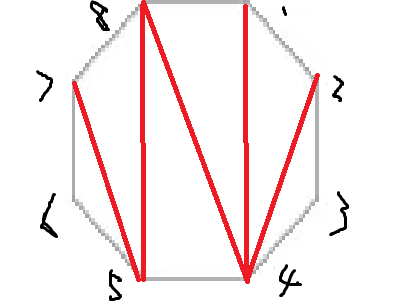
$\mathcal A$ is a collection of combinatorial objects. => $\mathcal A$ and $\mathcal B$ are combinatorically isomorphic if there exist a size-preserving bijection between $\mathcal A$ and $\mathcal B$ Q1 Prove that number of Dyck Paths D_{n-1} equa……

考虑空气阻力的竖直上抛问题 由于这篇blog语言儒雅随和通俗易懂，所以一般通过观众也可以放心观看 阻力 f=mkv^2, 其中m为物体质量，k为常数 阻力始终与运动方向相反 重力加速度为g 以初速度 v_0 将该物体上抛，试描述其运动速度与时间的关系 Answer: 首先因为阻力的方……

由于这篇blog语言儒雅随和通俗易懂，所以一般通过观众也可以放心观看 例题（著名题）： $\int^{\infty}{0}{\frac{{e^{cosx}}{sin(sinx)}}{x}}dx这道题乍一看很复杂，但其实在回顾过3B1B的傅里叶变换后，才发现这是一道可以用傅里叶级数暴力的题 首先介绍此题要用到的……

$$e^{ix}=cosx+isinx$$ $$\int_0^{\infty} {\frac{sinx}{x}} {\rm d}x=\frac {\pi}{2}$$ $$\iint {f(x,y)d\sigma}=\int{d\theta}\int{f(r,\theta)dr}$$ $$wordpress　nmsl$$

我佛了，空气阻力太难力 111 空气阻力F=kv^2 所以1° 上升时 F=-kv^2-mg dv/dt=-kv^2/m-g ∫(-1/kv^2/m+g)dv=t+v0 左边应该是arctan,所以v=-tanCt+v0，，， 2° 下降时 F=mg-kv^2 ∫(1/mg-kv^2)dv=t+C 有理分式……

是我，高斯男孩 e**** d*** integral ∫(-inf,inf)e^(-x^2)dx ← 这是高斯积分 原式^2 =∫(-inf,inf)e^(-x^2)dx*∫(-inf,inf)e^(-y^2)dy =∬e^(-x^2-y^2)dσ D={(x,y)|x∈R,y∈R} = ∫dθ∫re^(-r^2*sin^2θ-r^2*cos^2)dr D={(r,θ)|r∈[0,inf),θ∈[0,2π]……