2小时，100分满分，内容是图论，开卷，可带电子设备，可查阅课程笔记和资料，不可上网。点击长图查看：

大家好，这里是潜水已久的Zzzyt。虽然高考已经烂完了，NJU上不了一点，但是综评已经交了钱，不得不品尝，当作旅游罢了。 笔者报考的是 特长类 计算机科学与技术 笔者考场应到36人，实到28人。计科似乎有三个考场。 试题回忆 去年真题传送门 居然改题型，狡猾！！题目……

It's a well-known fact that the alternating groups, A_n, are simple for n\neq 4, with small cases like A_1, A_2, A_3 very easy to verify. Yet most proofs of n\geq 5, including Hungerford's, relies heavily on 'magical' permutation composition, which……

This proof is due to Arturo Magidin. In category theory, as we don't consider the 'internal structure' of objects, many properties of maps are defined in an abstract way using interaction with other morphisms. 'Epimorphism' is such an analog of sur……

题目背景 南大几把选拔中最水的题(T3), 适合出在初中竞赛里. 另外这期写解答方便以后想考南大几把的学生?, 篇幅太长除了题面不写中文了. 不过题面也是pmt提供的, 不一定完全准确. 题面 记排列P的置换环数量为c(P),排列P,Q的复合记为P\oplus Q，已知长度为n的排列f_1,f……

_wordpress又**了, 喜欢我pdf吗_

题目背景 贴吧范畴论帅哥问的一道题, 题目还算基础, 不过确实很容易伪证, 是名副其实的脑筋急转弯. 题面 对一个拓扑空间X, 定义集合S为稠密集当且仅当\text{Cl}(S)=X, R为无处稠密集当且仅当X-\text{Cl}(R)为稠密集. 定义集合A的边界\text{Bd}(A)=\text{Cl}(A)\cap\te……

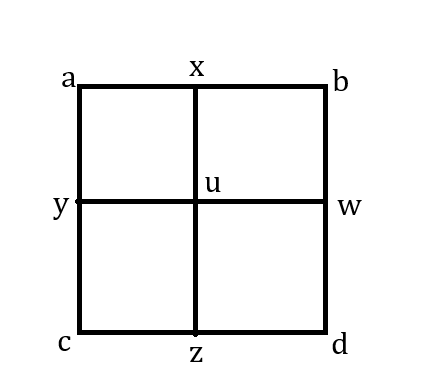
题目背景 总有人喜欢在高考数学中嚷嚷"仿射变换", 于是一道纯正射影几何高考"创新题"应运而生(其实还顺便测试一下QuickLaTex). 题面 如上图, , , 共线, , , 共线, , , 共线, 且, , 不共线, , , 不共线. (1) 若与不是同一平面, 求证与的交点, 与的交点, 与的交点共线.……

本文pdf链接

本文pdf链接