Dr.Jing's Lecture Note Ep.2
OGF - Cayley Formula
Question Statement
Prove # of trees on [n] = n^{n-2}
Solution
f:(1,2,3,...,n)\to(1,2,3,...,n)
f(1)=1,f(n)=n
Functional Digraph(directed graph) D
V(D)=[n] 编者注:V为节点集合
(i,j)\in E(D) if f(i)=j 注:E为边集合
Example
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| -- |
| f(x) | 1 | 5 | 3 | 11 | 10 | 12 | 5 | 15 | 12 | 7 | 1 | 7 | 15 | 3 | 15 |
The graph looks like follows:
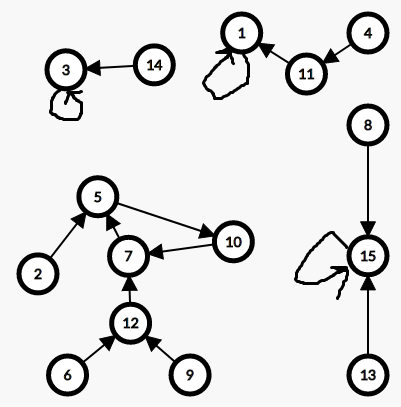
将环用最小的点表示并且拆环,得:
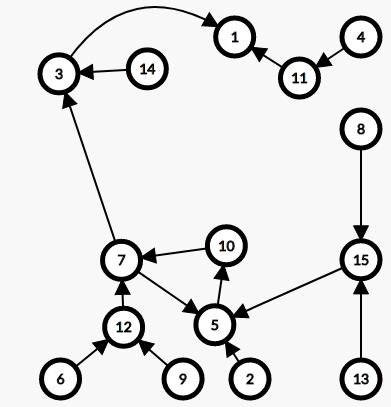
Permutation: Cycle Rep
Example Of Cycles
in (^{id=1,2,3,4,5,6,7,8,9}_{va=4,6,1,7,5,2,3,9,8})
cycles are (1,4,7,3)(5)(2,6)(8,9)
Problem Statement
C(n,k) is the # of permutations of n with k cycles.
Prove \sum_{i=1}^nC(n,k)x^k=\prod_{i=1}^n(x+i-1)
Solution
Let Cu(x)=\sum_{i=1}^nC(n,k)x^k=\prod_{i=1}^n(x+i-1)
将最小数设为Cycle的代表:如上例(1,4,7,3)(2,5)(8,9)(5)
按最小数逆序排序Cycle(8,9)(5)(2,6)(1,4,7,3)
\sum_{i=1}^nC(n,k)x^k=[x^k]Cu(x)
\prod_{i=1}^n(x+i-1)=x(x+1)(x+2)...(x+n-1)
Example
| step | choose | cycles |
| -- |
| 1 | x | (1) |
| 2 | x | (1)(2) |
| 2 | 1 | (1,2) |
| 3 | x | (3)(2)(1) |
| 3 | 2 | (2,3)(1) or (2)(1,3) |
即,若取x=newCycle
取常数=加到原来的一个环中
Another Problem
Problem Statement
S(n,k)=# of partitions of n elements into k blocks(顺序不重要) (不能为空)
Prove S(n,k)=\frac{1}{k!}\sum_{i=0}^k(-1)^k\binom{k}{i}(k-i)^n
Solution
\frac{1}{k!} 顺序不重要
\sum_{i=0}^k 枚举至少i个为空
\binom{k}{i} 选i个
(k-i)^n 随便放东西
Prove Problem I
Problem Statement
Prove A(n,k)=\sum_{i=0}^k\binom{n+1}{i}(k-i)^n (A(n,k) is # of permutations with k runs)
Solution
\sum_{i=0}^k空run的个数
两次容斥
Prove Problem II
Problem Statement
Prove D(n)=n!\sum_{k=0}^n\frac{(-1)^k}{k!}
D(n):# of permutations with no fix points(错排)
Solution
D(n)=\sum_{k=0}^n\frac{n!}{k!}\times(-1)^k
(-1)^k 容斥
\frac{n!}{k!}是A^{n-k}_n
k枚举多少个在自己位置上
Homework
Q1
find # of planar graph (labelled) on N nodes.
(Please see the O.Gimenei and M.Noy Asymptotic enumeration and limit laws of planar graphs J.A.M.S,2009 for answers.)
Q2
find # of unlabelled planar graphs on N nodes. Problems Open(Unsolved By Everyone)
Contact the teacher
版权声明:
作者:XGN
链接:https://blog.hellholestudios.top/archives/220
来源:Hell Hole Studios Blog
文章版权归作者所有,未经允许请勿转载。

共有 0 条评论