考虑空气阻力的竖直上抛问题

由于这篇blog语言儒雅随和通俗易懂，所以一般通过观众也可以放心观看
阻力 f=mkv^2, 其中m为物体质量，k为常数
阻力始终与运动方向相反
重力加速度为g
以初速度 v_0 将该物体上抛，试描述其运动速度与时间的关系

Answer:
首先因为阻力的方向不确定，所以要分两段处理↓↓↓

上升段

v'=-g-kv^2
\frac{dv}{dt}=-g-kv^2
\frac{dv}{g+kv^2}=-dt
\int{\frac{1}{g+kv^2}}dv=-t
令w=\sqrt{\frac{k}{g}}v
\int{\frac{1}{g+kv^2}}dv
=\frac{1}{g}\int{\frac{1}{1+\frac{k}{g}v^2}}dv
=\frac{1}{g}\int{\frac{1}{1+wv^2}}dv
=\frac{1}{g}\int{\frac{1}{1+wv^2}}d\sqrt{\frac{g}{k}}w
因为 \int{\frac{1}{1+x^2}}dx=tan^{-1} x+C
=\frac{1}{g}\sqrt{\frac{g}{k}}tan^{-1}w+C
=\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v)+C
因为当 t=0 时 v=v_0
所以 C=-\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v_0)
回到原式
\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v)+C=-t
tan^{-1}(\sqrt{\frac{k}{g}}v)=-\sqrt{kg}(t+C)
\sqrt{\frac{k}{g}}v=tan(-\sqrt{kg}(t+C))
v=\sqrt{\frac{g}{k}}tan(-\sqrt{kg}(t+C))
把 C 带入
v=\sqrt{\frac{g}{k}}tan(-t\sqrt{kg}+tan^{-1}(\sqrt{\frac{k}{g}}v_0))

那么我们分个段吧

找到v=0时t的值
在上升段中
v=\sqrt{\frac{g}{k}}tan(-t_1\sqrt{kg}+tan^{-1}(\sqrt{\frac{k}{g}}v_0))=0
tan(-t_1\sqrt{kg}+tan^{-1}(\sqrt{\frac{k}{g}}v_0))=0
明显tan 0 = 0
-t_1\sqrt{kg}+tan^{-1}(\sqrt{\frac{k}{g}}v_0)=0
tan^{-1}(\sqrt{\frac{k}{g}}v_0)=t_1\sqrt{kg}
t_1=\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v_0)
那么这个t_1就是分段依据了

下降段

和上升段毫无差别
所以我不做了
同理:
v'=-g+kv^2
\frac{dv}{dt}=-g+kv^2
\int{\frac{1}{g-kv^2}}dv=-t
这时候奇妙的函数出现了! \int{\frac{1}{1-x^2}}dx=tanh^{-1} x+C
易证得
=\frac{1}{\sqrt{gk}}tanh^{-1}(\sqrt{\frac{k}{g}}v)+C
因为当v=0时t=t_1
\frac{1}{\sqrt{gk}}tanh^{-1}(\sqrt{\frac{k}{g}}v)+C=-t_1=-\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v_0)
v=0
所以
C=-\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v_0)
所以说这个C和前面那个C一毛一样,,,
由于找预期非常懒，此处再次跳过带回原式的过程
v=\sqrt{\frac{g}{k}}tan(-t\sqrt{kg}+tanh^{-1}(\sqrt{\frac{k}{g}}v_0))
不就多了一个h吗...

OK 终极总结

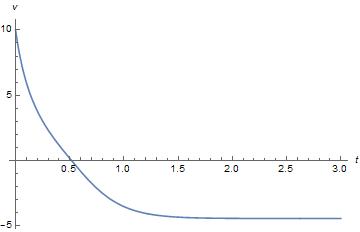
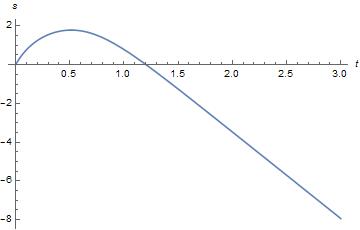
v = \begin{cases} \sqrt{\frac{g}{k}}tan(-t\sqrt{kg}+tan^{-1}(\sqrt{\frac{k}{g}}v_0))&0\le t<\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v_0)\\\sqrt{\frac{g}{k}}tan(-t\sqrt{kg}+tanh^{-1}(\sqrt{\frac{k}{g}}v_0))&t\ge\frac{1}{\sqrt{gk}}tan^{-1}(\sqrt{\frac{k}{g}}v_0) \end{cases}

Bonus!!!

Mathematica绘制的函数图象
k=0.5,g=10,v_0=10