大家好，这里是潜水已久的Zzzyt。虽然高考已经烂完了，NJU上不了一点，但是综评已经交了钱，不得不品尝，当作旅游罢了。

笔者报考的是 特长类 计算机科学与技术

笔者考场应到36人，实到28人。计科似乎有三个考场。

试题回忆

去年真题传送门

居然改题型，狡猾！！题目变得巨长

考试时间2小时

1.(20pts) 平面中有n个半径为1的圆，有一正方形S，使得以S中任意一点为圆心所作的半径为1的圆与已有的n个圆中的至少一个相交或重合。证明S的面积不大于4n\pi。

2.(20pts) x满足x+\frac{1}{x}=1。设t=x^{2024}+\frac{1}{x^{2024}}。比较\sqrt[2024]{(2023-t)!}和\sqrt[2023]{(2024+t)!}的大小。

3.(20pts) 有一田字格形的无向图如下：

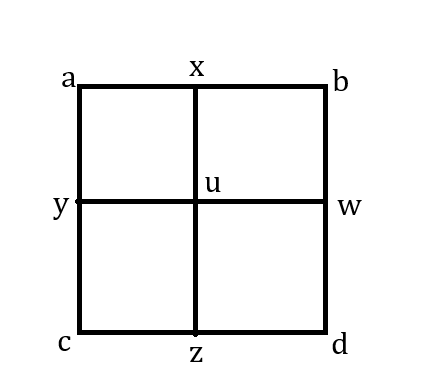
每个顶点标一个实数，其中a,b,c,d为常数
设\vec{r}=(x,y,z,w,u)，定义E(\vec{r})=\sum_{i,j}(i-j)^2，其中i,j遍历每条边两个端点上的标的数（即i,j \in \{a,b,c,d,x,y,z,w,u\}）。
求\vec{r_0}=(x_0,y_0,z_0,w_0,u_0)使得\forall \vec{r}, E(\vec{r}) \geq E(\vec{r_0})

4.(20pts) 对于m \geq 3，有定义域C_m=\{1,2,3...m\}。对于函数u(k):C_m \rightarrow \mathbb{R}，有算子\mathcal{L}：

\mathcal{L}u(k)=2u(k)-u(k-1)-u(k+1)

（规定u(0)=u(m)，u(m+1)=u(1)）。
若存在u(k),\alpha \in \mathbb{R}使得\mathcal{L}u(k)=\alpha u(k)，则称\alpha为\mathcal{L}的一个特征值。

(1) 写出\alpha=0时所有的u(k)

(2) 证明\mathcal{L}的所有特征值\alpha\in[0,4]

5.(20pts)有一凸n边形A_1A_2...A_n，其内部有一点P。设\alpha_i=\angle A_iPA_{i+1} （i=n时\alpha_i=\angle A_nPA_1）。
证明

\sum^{n}_{i=1}\cot\alpha_i \geq \sum^{n}_{i=1}\cot A_i + \frac{n}{\sin\frac{2\pi}{n}}