技术
-
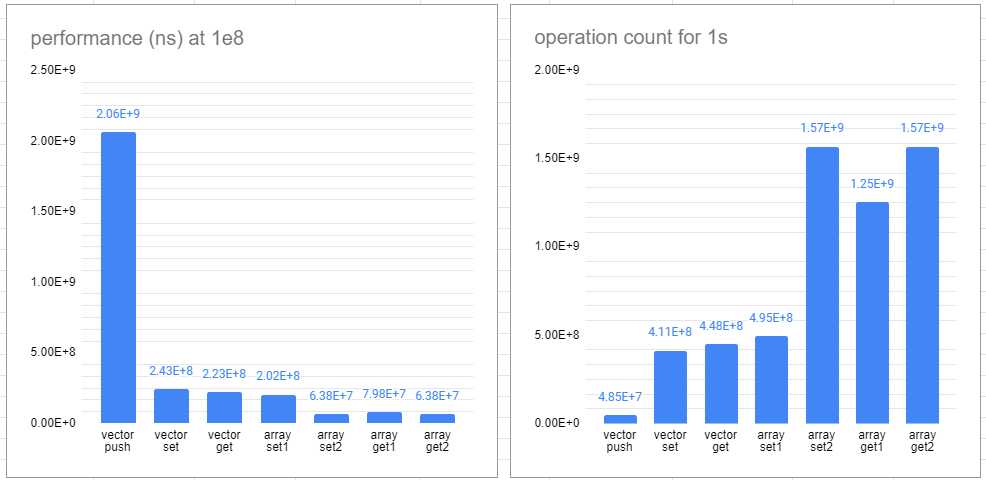
【OI的里技#2】vector测速
0.声明 算法第一 常优第二 C++是算法的载体,为算法服务。本系列的目的不在于推崇常优,而是解除OIer对常数的顾虑而专注于算法。 环境 编译参数 语言标准 优化等级 NOIP(2020) i7-8700K @3.70GHz 32GNOI Linux 1.4.1gcc 4.8.4 -lm c++11 O0 NOIP(2021+)…… -
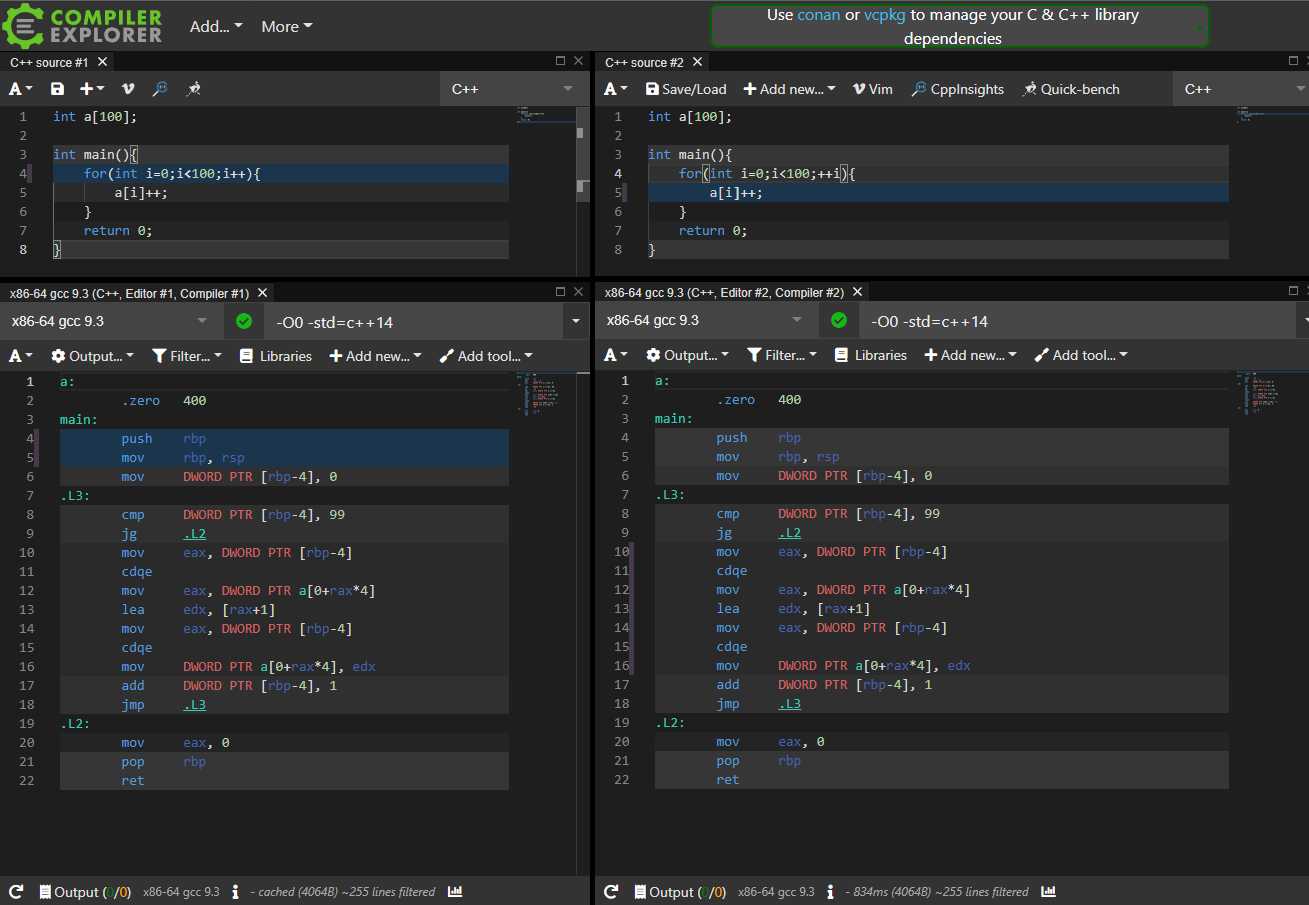
【OI的里技#1】常优分析: inline? register?
0.声明 算法第一 常优第二 C++是算法的载体,为算法服务。本系列的目的不在于推崇常优,而是解除OIer对常数的顾虑而专注于算法。 环境 编译参数 语言标准 优化等级 NOIP(2020) i7-8700K @3.70GHz 32GNOI Linux 1.4.1gcc 4.8.4 -lm c++11 O0 NOIP(2021+)…… -
Upload to Hell Hole Studios Blog - Howto
By XGN from Hexo Note: This article is for uploading to Hexo and is outdated (probably for now) The HHS new blog has been deployed for almost half a year, yet there are still some people who don't know how to upload blog. Here's a tutorial &a…… -
Modding and Adding Characters to Pressing Competition 2
From XGN Blog. Read it here Introduction Pressing Competition 2 or Typing Competition 2 is a Godot game which allows you to choose characters and fight against each other. It's open-sourced under MIT here You can find the showcase here It's dev…… -
优雅地使用Cloudflare自选ip优化Xray上网体验
By XIZCM from Hexo 我们知道,cloudflare作为全世界最大的CDN供应商,在全球分布着很多数据中心,且能免费使用。 那么,有没有可能用其来优化科学上网体验呢? 答案是有 首先在申请一个域名,并将其放在cloudflare解析 添加一个A类型解析到自己vps的ip,并打开cdn…… -
使用Idea的Java to Kotlin功能攻略Kotlin Round
From XGN Blog. You can also pay a visit to XGN's blog 笔者在Kotlin Hero3中采用这种方法获得了top50的好成绩,为了让更多人了解到这个作弊技巧,特写此文。 目标 在不学Kotlin或基础语法不牢固的情况下在Kotlin Hero比赛中取得优异的成绩。 前置条件 Intell…… -
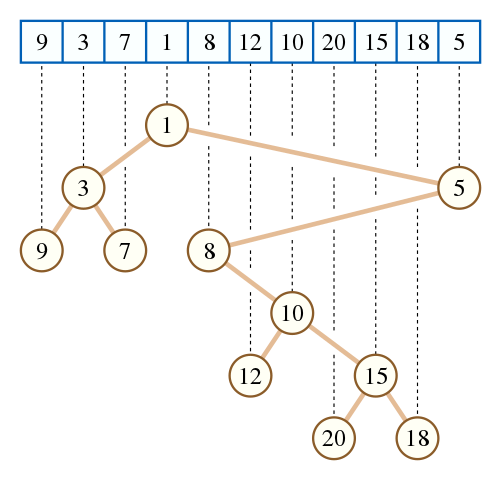
一种基于笛卡尔树的不稳定RMQ算法(玄学树)
本文原未备份,在迁移到Hexo的过程中丢失。然而笔者在自己的手机中偶然发现一份副本,遂复原至新站。 本文发布时间仅精确到天。 以下为原文。 序 某一天早上我突然突发奇想弄了一个奇怪的数据结构...然后查了查发现就是笛卡尔树... 不过查询方法非常神奇,非常暴力,…… -
浅谈薛定谔方程的不含时解
如题,本文适合轻度装X不甚深入,可放心食用 前置知识: - 偏导数 - 复数(以及欧拉公式) - 仅需常微分方程即可 - 基本的量子力学常识 让我康康 一维空间中的薛定谔方程(含时)长这个样子: i\hbar\frac{\partial}{\partial t}\Psi(x,t)=-\frac{\hbar^2}{2m}\frac{…… -
[神必函数]#3.神必的迭代函数
众所周知,有 x_{n+1}=r \cdot x_n(1-x_n) 这么一个东西,叫做单峰映像。 该函数具有神必的性质:分叉,如图所示: 由于该函数过于著名,有大量有关文章,因此再此不再讨论(赶紧去读Wikipedia啊) 而本文讨论的是x_{n+1}=x_n - r sin x_n,该函数与单峰映像有许多共…… -
[小小开发] python缓存
最近在写API,因为算力和调用别的API也有限制(大嘘,所以进行一个cache是很有必要的 本来以为这是一个非常简单的事情,就没有想到要调用轮子,最后发现实现的非常不优雅,, 惊讶的发现网上竟然有轮子 使用方式非常简单 安装包: pip3 install werkzeug 初始化: from……