题&解
-
狂暴野蛮人[1] 一阶线性非常系数微分方程
文明一思考, 野蛮就发笑 本系列着重使用暴力的手法去解决标答巧妙但很难想到的题, 内容多半为物理(因为物理本身就极其暴力), 可能会夹带少量数学; 暴力解法纯粹图一乐, 该学习的还是要学, 切勿因"一招鲜"而放弃思考! 1 (2022-2-27) 先置知识 求解一阶线性非常系数…… -
Orange Boy Can You Solve It Out? Ep.18.5 (the lost obcysio)
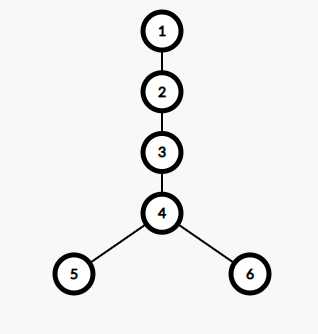
Solved! Difficulty: Div2D-Div2E Note: this problem is drafted on 2019/7/30 by XGN and not released. It's now released on 2022/1/2 by Zzzyt under his permission. Statement Yuqi has an rooted indexed tree T of N nodes indexed from 1 to N. The n…… -
Orange Boy Can You Solve It Out? Ep. 49
思考题 so easy just to prove I am not dead ESL Wulpit is a divine fox spirit. She is learning Chinese. So she doesn't understand English. One day she received an English string S of n lower case characters. XGN told her how her name would be like i…… -
Orange Boy Can You Solve It Out? Ep. 48
思考题 with git Version Control You are given a DAG with N nodes and M direcitonal edges. Node 1 has 0 in degree. We define a node i is required for node j if i is in any path from 1 to j. You are given Q queries, for each query you are given A and…… -
Orange Boy Can You Solve It Out? Ep. 47
Solved! Difficulty: Div2D Long time no see 思考题 Tree Traversing Hikari has a tree of N nodes. The node #1 is the root. Initially she is at node 1. She can do one of the following three operations: - Move to any adjacant node with cost 1 - M…… -
Crimson boy[5] 笑了
题目背景: 来自中等数学2021.4数学奥林匹克问题, 可能是这个栏目下有史以来最水的题, 以下解法非标答(因为没买No.5), 或许略显繁琐 题目: 设实数x_i(i=1,2,..,n)使得\sum_{i=1}^{n}x_i=0且\sum_{i=1}^{n}x_i^2=n(n-1). 证明: |\sum_{i=1}^nx_i^3|\leq n(n-1)(n-2) …… -
Crimson boi can u solve it?[4] 搞笑求积
题目背景: 在t教师课后, w同学提出此问题. 在现场的我由于过于弱智, 没能及时想出思路. 在回家途中准备展开时, 却无意中发现了"绝妙"的突破口. :i 题目: 求\prod_{i=1}^{n}(1+cos\frac{2i\pi}{n}) 先想再看提示哦 提示: 切比雪夫多项式 …… -
Orange Boy Can You Solve It Out? Ep. 46
chemistry 思考题 Hydrocarbon Ninetail is building a tree. She has N nodes and she will assign a value from 0 to 3 to each node. All nodes with the same value are indistinguishable. Then she will connect the N nodes with N-1 edges so that they form …… -
Orange Boy Can You Solve It Out? Ep. 41-43
OBCYSIO Ep.41 to 43 is hosted on XGN's blog. As I am lazy to copy, please read them here -
Orange Boy Can You Solve It Out? Ep. 45
From Hexo Useful 思考题!! Replace Hikari is a cute white dragon girl. She is helping Ninetail - a fox girl, her master - correct composition.The original composition is a string S and the corrected one is another string T. Hikari claimed that……

![狂暴野蛮人[1] 一阶线性非常系数微分方程](https://s1.ax1x.com/2022/04/17/LN0AnH.png)

![Crimson boy[5] 笑了](https://blog.hellholestudios.top/wp-content/uploads/2021/06/kc.jpg)