教程
-
NUS Japanese Placement Test 心得
Context 笔者作为交换生报名了新加坡国立大学的日语课程,由于曾经参加过日语训练,需要参加日语Placement Test。参加链接如下:CLS。 作为参考,笔者的阅读水平为N2,听力水平为N3,但是由于参加的是应试课程,没有口语和写作经验。 筆者は交換留学生として、会話と…… -
Small note on Large models - 0. Introduction
This new series is primarily a continuation of the old series Test Logic with a slightly different flavour, namely it focuses on a very concrete and special axiom system - ZF set theory. Note that old chapters might be updated as well. 0.0 Introduc…… -
一种基于反向RPC的简易可重连通用的非延迟重视型单权威服务器客户端架构的多人游戏实现
没错 本文标题就是搞笑的 前言 相比较单机游戏,联网多人游戏要考虑的事情就多了:如何在多个玩家之间正确的同步游戏状态、如何处理玩家掉线和重连、如何防止网络延迟给玩家带来的不好体验。因此,编写多人游戏时,其业务逻辑常常比单人游戏更加复杂,许多时候不得不…… -
具身智能简单概述
在具身智能成为国家新型发展战略的当下,本文尝试完整梳理具身智能的技术路线。 原文链接: https://ys.al/post/17 声明 本文大部分观点出自:https://github.com/HCPLab-SYSU/Embodied_AI_Paper_List 具身机器人 具身机器人作为智能和外界互动的主要部分。 固定底…… -
-
crimboi[22] 你什么拓扑?
funny problem from model theory problem sheet 题面 Let L be a countable language, T a theory. Let c_1,c_2,... be new constants, L'=L\cup\lbrace c_1,...\rbrace, and let X be the set of all complete theories of L' with T\subset t. Enumerate the L' se…… -
一种无递归、无栈、无parent指针的红黑树实现
前言 红黑树是一种复杂的平衡树,在大部分情况下都会使用父指针或者递归实现。假如我们一定要三无实现呢? 本文必须配合OI-Wiki食用!! 基础结构 #define BLK_COLOR 0 #define RED_COLOR 1 #define LEFT 0 #define RIGHT 1 #define Color(node) (node==NULL?BLK_COLO…… -
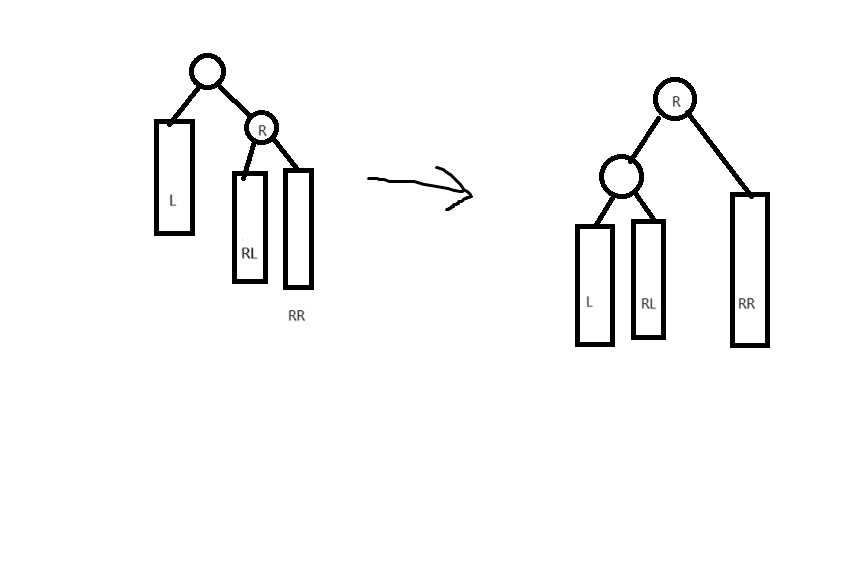
一种基于维护高度的无递归、无栈、无parent指针的AVL树实现方式
感谢XLH同学指出blog中的一些错误,本文已于2024/9/28更新 引入 AVL树有种种实现方式,其中最自然的是采用递归的写法,毕竟AVL树是递归定义的。但是,有的老师认为“递归时间常数大”,觉得应该用迭代。但是,还有老师认为迭代要用栈,“栈空间大(指占用了 O(\log n) )…… -
crimboi[21] 模仿大赛
Rotman algebraic topology上的题, 个人认为出的非常好, 极大增进了读者对\pi_1(S^1)计算过程的理解. 题面 A group G which is also a topology space is called a topological group if \mu:G\times G\to G:(x,y)\mapsto xy and i:G\to G:x\mapsto x^{-1} are contin……



![群论简介[2] 群作用!!!](https://blog.hellholestudios.top/wp-content/uploads/2025/05/57.group-actions-v2.png)
![群论简介[1] 群的相关定义](https://blog.hellholestudios.top/wp-content/uploads/2025/04/OIP-C.jpg)
![crimboi[22] 你什么拓扑?](https://blog.hellholestudios.top/wp-content/uploads/2024/11/Pasted.jpg)
![crimboi[21] 模仿大赛](https://blog.hellholestudios.top/wp-content/uploads/2024/09/Pasted.jpg)