狂暴野蛮人[1] 一阶线性非常系数微分方程

文明一思考, 野蛮就发笑

本系列着重使用暴力的手法去解决标答巧妙但很难想到的题, 内容多半为物理(因为物理本身就极其暴力), 可能会夹带少量数学;

暴力解法纯粹图一乐, 该学习的还是要学, 切勿因"一招鲜"而放弃思考!

1 (2022-2-27)

先置知识

求解一阶线性非常系数微分方程$\dot{y}=f(x)y+g(x)$:

首先既然它是线性的, 很容易想到先求其次的通解, 即先解$\dot{y}=f(x)y$; 容易解出, 它的解为$y=Ce^{\int f(x)\mathrm{d} x}$.

于是原方程的解应为$y=Ce^{\int f(x)\mathrm{d} x}+\hat{y}$, 其中$\hat{y}$也满足$\dot{\hat{y}}=f(x)\hat{y}+g(x)$.

当两边同乘$e^{-\int f(x)\mathrm{d} x}$后, $ye^{-\int f(x)\mathrm{d} x}=C+\hat{y}e^{-\int f(x)\mathrm{d} x}$; 我们也许可以猜想$ye^{-\int f(x)\mathrm{d} x}$是一个不定积分的结果.

尝试对它求导: $\dot{(ye^{-\int f(x)\mathrm{d} x})}=\dot{\hat{y}}e^{-\int f(x)\mathrm{d} x}-f(x)\hat{y}e^{-\int f(x)\mathrm{d} x}=g(x)e^{-\int f(x)\mathrm{d} x}$, 这验证了我们的猜想!

于是$ye^{-\int f(x)\mathrm{d} x}=\int g(x)e^{-\int f(x)\mathrm{d} x}\mathrm{d}x$.

题面

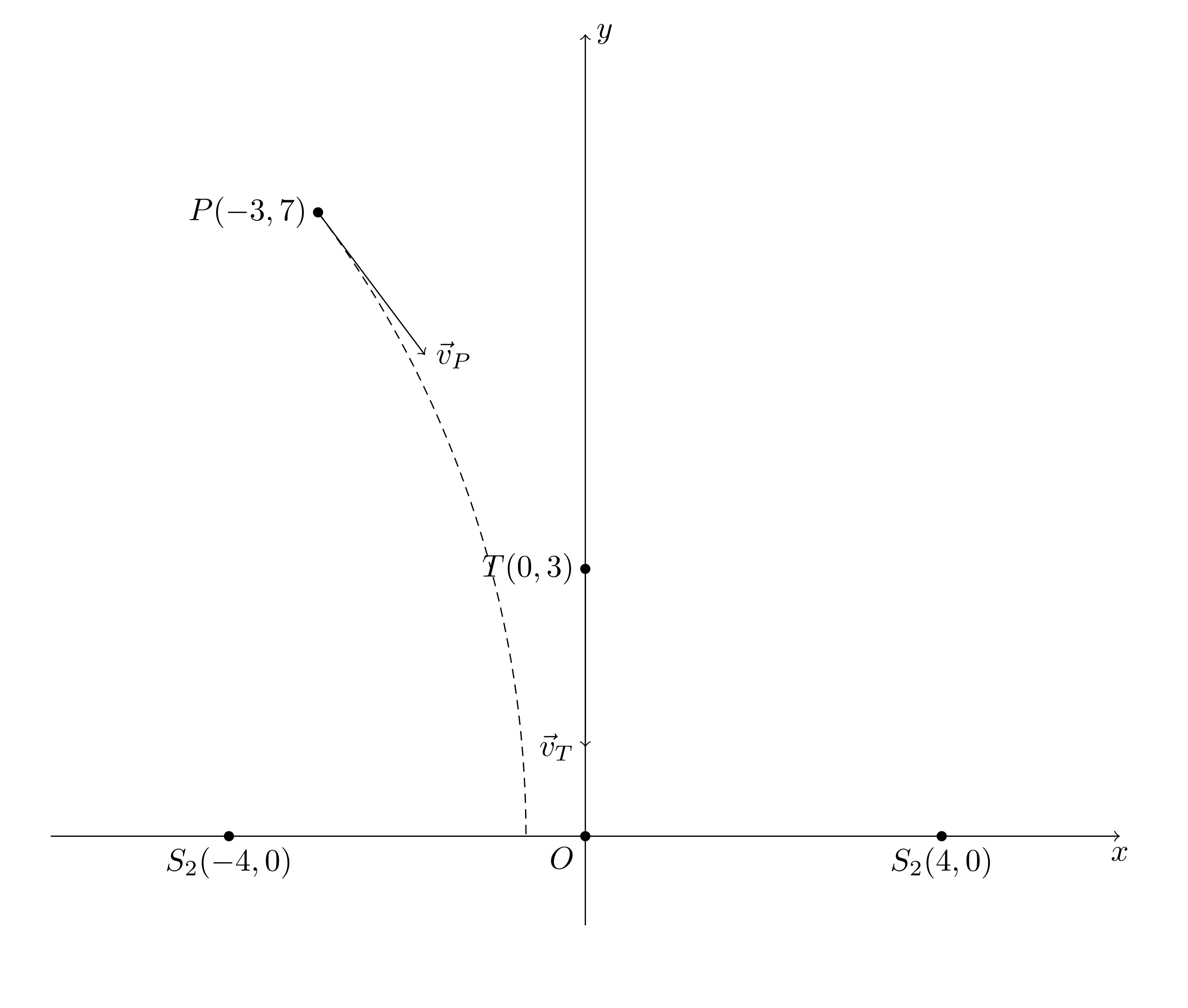
如图, 在$(-4,0)$与$(4,0)$处分别有警亭$S_1$, $S_2$. 一小偷$T$在$(0,3)$处行窃. $t=0$时刻, 在$(-3,7)$处的警察$P$发现了小偷, 并立刻开始追逐小偷, 警察的速度矢量始终和他与小偷位置的连线共线. 小偷因害怕警亭内有警察, 选择如下逃跑方法: 保持自己到$S_1$, $S_2$, $P$三者的距离相等. 求警察的运动轨迹.

评论

见过这题的人都应该记得$P$在一个阿氏圆上, 但对初见来说很难想到考察$|PS_1|$与$|PS_2|$的关系, 毕竟它们的坐标表示是极其复杂的. 对数学基础不好的人来说, 这题列出微分方程后就解不下去了(高中物理竞赛确实不需要学生掌握一阶线性非常系数微分方程). 但别急! 对有着先置知识的我们来说, 解出方程简直是小菜一碟.

题解

由小偷保持自己到$S_1$, $S_2$距离相等得小偷沿$y$轴逃跑, 于是可设$T\coloneqq (0,t)$; 再令$P \coloneqq (x,y)$.

据小偷保持到$P$与到$S_1$, $S_2$距离相等可得$x^2+(y-t)^2=4^2+t^2$; 解得$t=\frac{x^2+y^2-16}{2y}$.

由警察速度始终朝着小偷得$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{y-t}{x}$; 带入上面解得的$t$得到$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{y^2-x^2+16}{2xy}$.

分母的$xy$十分恼人, 想办法将其变成$x^2$或$y^2$使得右边是关于$x^2,y^2$的函数, 然后即可进行换元变成线性方程.

两边同乘$\frac{y}{x}$, 得$\frac{y\mathrm{d}y}{x\mathrm{d}x}=\frac{y^2-x^2+16}{2x^2}$; 为方便进行换元$X\coloneqq x^2$, $Y\coloneqq y^2$, 原式转化为$\frac{\mathrm{d}Y}{\mathrm{d}X}=\frac{1}{2X}Y+\frac{8}{X}-\frac{1}{2}$; 这是一阶线性非常系数微分方程, 其中$f(X)=\frac{1}{2X}$, $g(X)=\frac{8}{X}-\frac{1}{2}$.

依据先置知识中的解法, 先算$e^{-\int f(X)\mathrm{d} X}=e^{-\frac{1}{2}\ln X}=X^{-\frac{1}{2}}$.

那么$YX^{-\frac{1}{2}}=\int(\frac{8}{X}-\frac{1}{2})X^{-\frac{1}{2}} \mathrm{d} X=-X^{\frac{1}{2}}-16X^{-\frac{1}{2}}+C$.

带回$X=x^2$, $Y=y^2$, 即得$x^2+y^2+Cx+16=0$; 带入初值$(-3,7)$解得$C=\frac{74}{3}$, 那么轨迹方程就是$x^2+y^2+\frac{74}{3}+16=0$, 是一个圆心在$(-\frac{37}{3},0)$, 半径为$\frac{35}{3}$的圆, 这正是标答中的阿氏圆!