Orange Boy Can You Solve It Out? Ep.24
思考题 for China Birthday!
Military parade
It's going to be the 70th birthday of China! Orange Boy is looking forward to it and to celebrate this, he became Red Boy! So he proposes the following problem for you:
On Oct.1st. There is a military parade. The Beijing city can been seen as a 2D plane and each person in the parade can be seen as a single point. There are N people in the parade and the i-th of them is located at (x_i,y_i) initally.
On each second, each person will move down for 1 unit. That's to say, if a person initally at (x,y) will be at (x,y-t) after t seconds.
Our beloved Chairman Xi is located at (0,0) with an inital sight angle of 0 degree. If he has a sight angle of D degree, he will be able to see every person in the parade in the area which can be sweeped from the positive x axis by rotating D degree. He can see through people, means his sight will not be blocked by anyone.
For example, if Xi's sight angle is 45 deg, he will see the area(including the border line) below:
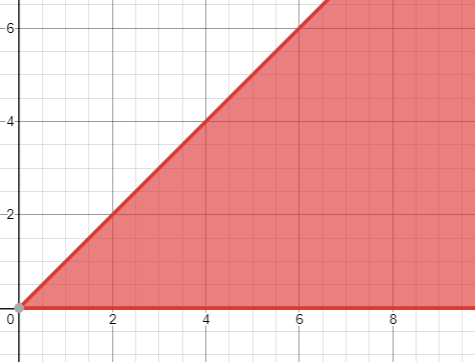
Now there are Q operations which you need to proceed them in a row.
- "hmcis x" if the time is at the x-th second, how many people can Xi see? The x is not necessarily increasing.
- "cmpov x" change the sight angle to x degree.
Proceed the queries.
Example
people = {{1,2},{3,4},{5,6},{1,0},{-10,-10}}
query={
hmcis 0,
cmpov 45,
hmcis 2,
cmpov 360,
hmcis 0
}
Output:
3
5
Explain:
At first, Xi's sight angle is 0, so he cannot see anyone.
Then after he changes his sight angle to 45.
Then at 2nd second, the plot looks like follow:
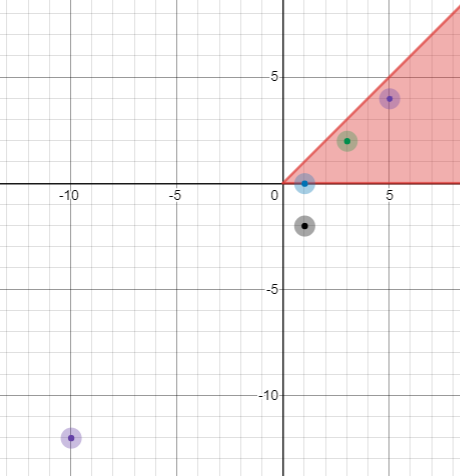
Then he changes his sight angle to 360.
Then he can see:
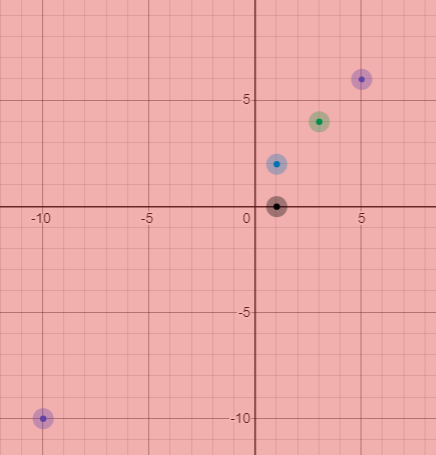
Constriants
Subtask 1: No query "cmpov"
Subtask 2: for all x in "cmpov x", x is a multiple of 45.
Subtask 3: q=1
Subtask 4: for all x in "cmpov x", x is a multiple of 30.
Subtask 5: for all x in "hmcis x", x=0
Subtask 6: for all x in "hmcis x", x is increasing
Subtask 7: for all x in "cmpov x", x is a multiple of 90.
Subtask 8: q,n<=1000
Subtask 9: 1\leq q,n\leq 10^5,1\leq |X_i|,|Y_i|\leq 10^9,X_i\in Z,Y_i\in Z. For any x in te queries, 0<=x<=1e9, x is an integer.
Can you solve it?
版权声明:
作者:XGN
链接:https://blog.hellholestudios.top/archives/287
来源:Hell Hole Studios Blog
文章版权归作者所有,未经允许请勿转载。

Peeper
TLE solution:
First we rewrite the queries in the form (t_i, theta_i), which means to ask the answer in the t th second with a sight angle theta.
Noticing the angle is always an integer, we take theta := theta mod 360, thus there will be only 360 possible values of theta.
Then it’s easy to observe and find that all the soldiers’ movement is equivalent to chairman Xi’s movement, so we can assum that the soldiers’ positions are fixed, and chairman’s position is (0, t) at time t.
So the sight of our great chairman is the area that is above line y = t and below line y = ax + t (Actually it’s not exactly like this, for example when theta > 90 degrees, we have a different situation. But that doesn’t make a big influence and this solution is still right.), where a is determined by theta.
Hence in the line y = ax + t, there’s no more than 360 possible values of a, and actually this number can be reduced to 180, as the line of theta and theta + 180 degrees are the same.
And when a is fixed, we know that P(x0, y0) is above y = ax + t <=> y0 > a*x0 + t <=> y0 - ax0 > t. So for each a we sort each point in the increasing order of y - ax, which means we can easily get the number of the points which are above or below a line using binary search.
Also the number of points which are below the line y = t can be easily got in the same way.
So till now, if we fix a and t and let the number of soldiers in the four areas divided by the two lines clockwisely be u, v, w and x, we can get the value of u + v, v + w, w + x and x + u. By solving the equations we can get u, v, w and x.
Then for each query we can get the answer.
Complexity summary:
1. In the precalculation, for each possible a, we sort all the points, as there’s 180 values of a, the total complexity of this part is O(180 * n * logn)
Then for each query, we binary search to get and solve the value of u, v, w and x mentioned above. The complexity of this part is O(q logn)
So the total complexity is O( ( 360 * n + q) logn). We take n = 100000 into this formula and get a result of nearly 576000000. As a lot of double calculation is involved, this algorithm will surely get TLE.
—— But if our nice author can increase the time limit to 10 seconds, this algorithm will pass.
(And I wonder whether Orange boy and XGN have a better solution, and also whether a solution exists if we remove the condition “ any x in queries is an integer”.