Solved!
Difficulty: Div2 C

思考题 in mid autumn

LianLi Branches

Wulpit has drawn n nodes(indexed from 1 to n) and n-m edges on paper for homework assignments. They form m rooted trees (aka a forest). However, when she went to the toilet, Fely came and added exactly m-1 edges so that the forest became a tree! The edges Fely drew and the edges Wulpit drew are not distinguishable which becomes a big trouble for Wulpit.

Luckily, Wulpit has marked out the roots for each tree: r_1, r_2, ..., r_m. She wants to know the following fact:
- For each edge in the final tree, could it be an edge added by Fely?
- For each node in the final tree, how many different trees could it belong to initially?

Example

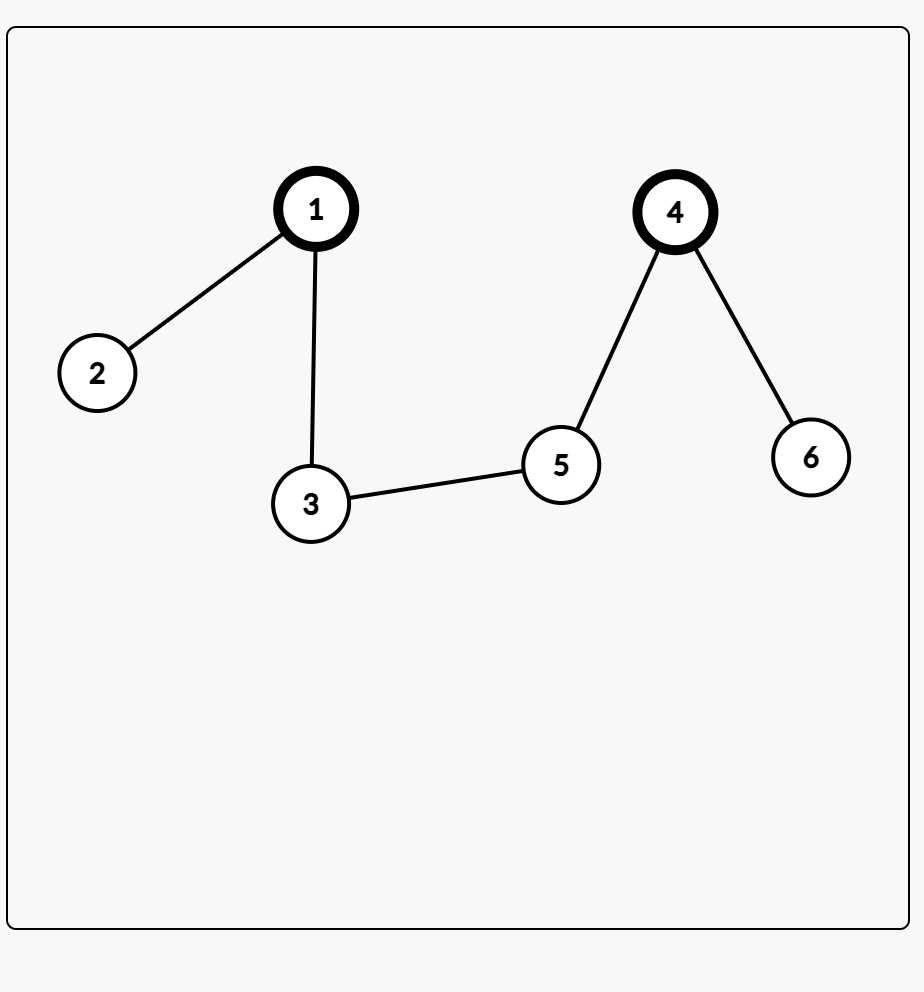
bold nodes are roots.

The tree can be interpreted as:

• tree{1,2} and tree{3,4,5,6}

• tree{1,2,3} and tree{4,5,6}

• tree{1,2,3,5} and tree{4,6}

So the edges possibly added by Fely are: 1-3,3-5,5-4

And,
- Node 1,2 can only belong to the root 1.

• Node 3,5 can belong to either root 1 or root 4.

• Node 6 can only belong to root 4.

Constraints

$n,m \leq 10^5$

Solution

By XGN:

An edge can be added by Fely if and only if it is in any path of two roots.

How many trees a node can belong to is the number of "adjacent" roots. Adjacent means the path from this node to the root does not contain any other roots.

Very easy, right? 😛