Dr.Jing's Lecture Note Ep.1

$\mathcal A$ is a collection of combinatorial objects.
=> $\mathcal A$ and $\mathcal B$ are combinatorically isomorphic
if there exist a size-preserving bijection between $\mathcal A$ and $\mathcal B$

Q1

Prove that number of Dyck Paths D_{n-1} equals to number of triangulations of a n-polygon T_n

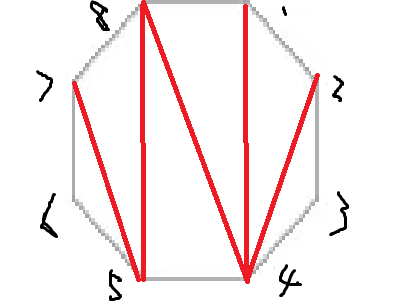
1. Label all the points

2. $3\le j \le n$
   if $(i,j)$ is an edge, $i\lt j$, then we draw an edge $E\uparrow$

3. Finish by drawing an E\to

OGF

$\mathcal A(x)=\sum_{i\ge0}a_ix^i$

Q2

a_n=2a_{n-1}-a_{n-2}+2^n,n\ge2
a_0=1,a_1=3
Find the value of a_n
\sum_{n\ge2}a_nx^n=\sum_{n\ge2}2xa_{n-1}x^{n-1}-x^2a_{n-2}x^{n-2}+2^nx^n
(\mathcal A(x)-3x-1)=2x(\mathcal A(x)-1)+x^2\mathcal A(x)+\sum_{n\ge2}(2x)^n
\mathcal A(x)=\frac{3x+1-2x+\frac1{1-2x}-1-2x}{1-2x+x^2}=\frac{1-x+2x^2}{(1-x)^2(1-2x)}=\frac B{1-x}+\frac C{(1-x)^2}+\frac D{1-2x}
1-x+2x^2=B(1-x)(1-2x)+C(1-2x)+D(1-x)^2
take x=1\rightarrow C=-2\x=\frac12\rightarrow D=4\x=0\rightarrow B+C+D=-1\rightarrow B=-1
a_n=x^n\frac{-1}{1-x}+\frac{-2}{(1-x)^2}+\frac4{1-2x}\\;\;\;\,=-1-2(n+1)+2^{n+2}=2^{n+2}-2n-3

HW

a_n=3a_{n-1}-2a_{n-2}+1,n\ge2
a_0=2,a_1=4
Find the value of a_n

Q4

\sum_k\binom m k\binom{n+k}m=\sum_k\binom m k\binom n k2^k
\sum_{n\ge0}x^n\sum_k\binom m k\binom{n+k}m=\sum_{n\ge0}x^n\sum_k\binom m k\binom n k2^k
LHS=\sum_k\binom m kx^{-k}\sum_{n\ge0}\binom{n+k}mx^{n+k}\\quad\quad\,=\sum_k\binom m kx^{-k}\frac{x^m}{(1-x)^{m+1}}\\quad\quad\,=\frac{\sum_k\binom m kx^{m-k}}{(1-x)^{m+1}}\\quad\quad\,=\frac{(1+x)^m}{(1-x)^m+1}
RHS=\sum_k\binom m k2^k\sum_{n\ge0}\binom n kx^n\\quad\quad\;=\sum_k\binom m k2^k\frac{x^k}{(1-x)^{k+1}}\\quad\quad\;=\frac1{1-x}\sum_k\binom m k(\frac{2x}{1-x})^k\\quad\quad\;=\frac1{1-x}(1+\frac{2x}{1-x})^m\\quad\quad\;=\frac{(1+x)^m}{(1-x)^m+1}

Q5

Prove \sum_{k\ge0}(-1)^{n-k}\binom{2n}k^2=\binom{2n}n

\sum_{m\ge0}\sum_{k\ge0}(-1)^{n-k}\binom{2n}k\binom{2n}{m-k}x^m\=\sum_k(-1)^{n-k}\binom{2n}kx^k\cdot\sum_m\binom{2n}{m-k}x^{m-k}\=\sum_k(-1)^{n-k}\binom{2n}kx^k\cdot(1+x)^{2n}=(-1)^n(1-x)^{2n}(1+x)^{2n}=(-1)^n(1-x^2)^{2n}
m is an even number

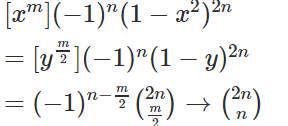
Q6

Prove \prod_1^\infty(1+x^{2i-1})=1+\sum_{k=1}^\infty\frac{x^{k^2}}{(1-x^2)(1-x^4)\cdots(1-x^{2k})} (Euler's Identity)

HW

Prove \prod_{i=1}^\infty(1+x^{2i})=1+\sum_k\frac{x^{k(k-1)}}{(1-x^2)(1-x^4)\cdots(1-x^{2k})}

Thm

The OGF's for partitions
using parts in {1,\cdots,k};
partitions with largest part k;
all partitions,are
\prod_{i=1}^k\frac1{1-x^i},\quad x^k\prod_{i=1}^k\frac1{1-x^2},\quad\prod_{i=1}^\infty\frac1{1-x^i}

Def

[n]={1,\cdots,n}
a run is a maximal increasing string in the word
84135726 has 4 runs: 8, 4, 1357, 26
The Eulerian number
A(n,k) is the number of permutations of [n] containing k runs.
A(n,k)=A(n,n+1-k)

Thm (Worpitzky's Identity)

x^n=\sum_{k=1}^nA(n,k)\binom{x-k+n}n
x^n: number of functions from [n] to
x boxes, there can be nothing in a box, or some balls in a box. If there are some balls in a box, then list the balls from small to large, like:
79|136|8||45|2
|79|13|68|45|2
791368452\to79|1368|45|2
x separates, k runs, so add x-k separates, there are \binom{x-k+n}{x-k}=\binom{x-k+n}n ways
so the answer is A(n,k)\binom{x-k+n}n

Thm

A(n,k)=\sum_{i=0}^k(-1)^i\binom{n+1}i(k-i)^n
\mathcal A(x)=\sum_kA(n,k)x^k
\mathcal B(x)=\sum_k\binom{k+n}nx^k
\mathcal A(x)\mathcal B(x)=\sum_l\sum_{k=1}^lA(n,k)\binom{l-k+n}{n}x^l\\quad\quad\quad\quad\,=\sum_ll^nx^l=\mathcal C(x)
\mathcal A(x)=\frac{\mathcal C(x)}{\mathcal B(x)}=(1-x)^{n+1}\cdot\mathcal C(x)
[x^k]\mathcal A(x)=\sum_{i+j-k}\binom{n+1}i(-1)^i