一种基于笛卡尔树的不稳定RMQ算法(玄学树)
本文原未备份,在迁移到Hexo的过程中丢失。然而笔者在自己的手机中偶然发现一份副本,遂复原至新站。
本文发布时间仅精确到天。
以下为原文。
序
某一天早上我突然突发奇想弄了一个奇怪的数据结构...然后查了查发现就是笛卡尔树...
不过查询方法非常神奇,非常暴力,但是非常快,但是非常不稳定...
网上有这种算法的代码,但是多半把它看做一种暴力,有博客甚至认为该算法复杂度O(logN)(下文会说明其实是O(1)),洛谷也没有相关题解,可见目前该算法并未得到应有的重视,故论证。
为了与正统的笛卡尔树+LCA区分,以下称该算法为玄学树。
思想
最大值RMQ和最小值RMQ是对称的,下文默认讨论最大值RMQ。
RT,该算法只适用于随机数据,如不随机会迅速退化。
对于随机数据,随机查询,显然查询区间通过全局最大值的概率很大(如果该数不在边缘)。所以可以判断查询区间是否经过全局最大值,然后可判断在最大值左边还是右边...以此类推。
能够实现上文算法的数据结构就是笛卡尔树。
笛卡尔树究其根本是个Treap,每个节点包含在原数组中的位置i与值a_i两种信息,其中位置满足二叉查找树的性质,值满足堆的性质。关于笛卡尔树的文章网上较多,在此不再赘述。
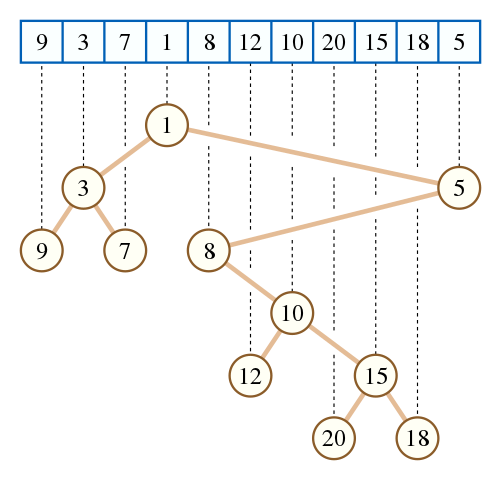
可以用单调栈维护右链(从根一直往右边跑)来O(n)建树,且常数极小。
查询时,从根开始,若查询区间经过根(最大值)则返回;否则判断查询区间在根左边还是右边,向下一层递归查询。非常显然。
均摊复杂度O(1)。
实现
Code:
int n;
int rt=0;
int l[MAXN*2],r[MAXN*2],a[MAXN*2];
int hsh(int x){
return (x*19260817)&((1<<20)-1);
}
int stk[MAXN*2];
void build(){
int top=0;
for(int i=0;i<n;i++){
int k=top;
while(k && (a[i]>a[stk[k]] || (a[i]==a[stk[k]] && hsh(i)>hsh(stk[k]))))k--;
if(k)r[stk[k]]=i;
if(k<top){
if(stk[k+1]==rt)rt=i;
l[i]=stk[k+1];
}
top=k+1;
stk[top]=i;
}
}
int query(int L,int R){
int x=rt;
while(x<L||x>R){
if(x<L)x=r[x];
else x=l[x];
}
return x;
}
注意hsh(x)是重要的,能够防止在不是很随机,有相同数字的数据下退化,能明显提高稳定性。
另外,用一个数组cache哈希值并不会变快很多,没有必要。
复杂度证明
由于笔者非常弱,此处给出不严格证明:
假如数据非常随机,以至于树是完全平衡的(实际上经常接近平衡):
我们枚举查询区间的左右端点a,b(可以有a>b,若如此可以自行翻转),若根的位置为\frac{N}{2},则:
a<\frac{N}{2},b>\frac{N}{2}的概率为\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}
a>\frac{N}{2},b<\frac{N}{2}的概率为\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}
所以查询区间经过根的概率为\frac{1}{4}+\frac{1}{4}=\frac{1}{2}。
同理在不经过根的区间中有\frac{1}{2}会经过根的一个儿子,以此类推。
所以预期访问节点数为
S=\sum_{i=1}^{\infty} \frac{i}{2^i}=\frac{1}{2}+\frac{2}{4}+\frac{3}{8}+\frac{4}{16}...
求该表达式的值:
易见得
2S-S = 1+\frac{2}{2}-\frac{1}{2}+\frac{3}{4}-\frac{2}{4}... =\sum_{i=0}^{\infty} \frac{1}{2^i} = 2
即S=2
可以发现查询复杂度为常数。
实测
读者可能会认为这么玄学的复杂度是假的,然而实际测试表明平均访问节点数确实在2~3左右,且与原数组长无关。
TODO
应用
使用玄学树可以吊打ST表,尤其是在查询次数不多时建树快的优势尤其大。
实际上洛谷ST表模板题排名第一的解法就是玄学树。
实际上这道题有大量OIer相互模仿使用玄学树。。。。。。。。
然后如果你去翻了翻顶上kcz rank1的代码,你发现他做到这里就结束了,底下是一个暴力查询.
---qwaszx的洛谷题解
通过欧拉序,LCA也可转化为RMQ,也可以用玄学树。
但是欧拉序数组不是非常随机,因此效果不好,但是还是能过的。
提交记录
如果你对出题人的道德水平充分信任,可以放心大胆地用玄学树
带修玄学树/离散玄学树
笛卡尔树其实是Treap,也可以用Treap旋转的方式进行修改。
复杂度依然平均O(1),最坏为树高。。。
这样玄学树就成了除线段树之外唯一一种支持修改的在线RMQ了。。
甚至可以处理离散的数组(e.g.大部分元素为-\infty的数组)。。
这样就吊打动态开点线段树了。。。
代码:TODO
版权声明:
作者:Zzzyt
链接:https://blog.hellholestudios.top/archives/558
来源:Hell Hole Studios Blog
文章版权归作者所有,未经允许请勿转载。

共有 0 条评论