一种基于维护高度的无递归、无栈、无parent指针的AVL树实现方式
感谢XLH同学指出blog中的一些错误,本文已于2024/9/28更新
引入
AVL树有种种实现方式,其中最自然的是采用递归的写法,毕竟AVL树是递归定义的。但是,有的老师认为“递归时间常数大”,觉得应该用迭代。但是,还有老师认为迭代要用栈,“栈空间大(指占用了 O(\log n) )空间”,不能用栈。自然,我们可以用parent指针规避掉这一问题,但是显然parent指针需要使用的额外内存更大,这位老师还是不喜欢。所以现在我们被要求实现三无AVL——无递归、无栈、无parent指针。
AVL树的维护方法有两种:维护高度和balance factor(BF)。笔者认为Balance Factor不够优雅、泛用性低、过于特殊化,故采用维护高度的方式。
注:其实,维护BF所需要的空间较小,在高度不会有其他作用时也可以优化空间维护BF。
所以,本文认为,三无AVL实现的重点在于 快速的维护每个节点子树的高度。
数据结构
struct AVL{
AVL* left;
AVL* right;
int value;
int height;
void print();
};
int Height(AVL* node){
return node==NULL? 0 : node->height;
}
void AVL::print(){
cout<<"(";
if(left!=NULL){
left->print();
}
cout<<value<<","<<Height(right)-Height(left); //get balance factor
if(right!=NULL){
right->print();
}
cout<<")";
}
void UpdateHeight(AVL* node){
node->height=max(Height(node->left),Height(node->right))+1;
}
旋转
AVL消除失衡的方式主要靠旋转,主要有左旋、右旋、double左旋、double右旋四种,具体的旋转方法请参考OI-wiki,我们仅给出旋转的实现:
//returns new root
AVL* RotateLeft(AVL* root){
AVL* r=root->right;
AVL* rl=root->right->left;
root->right=rl;
r->left=root;
UpdateHeight(root);
UpdateHeight(r);
return r;
}
//returns new root
AVL* RotateRight(AVL* root){
AVL* l=root->left;
AVL* lr=root->left->right;
l->right=root;
root->left=lr;
UpdateHeight(root);
UpdateHeight(l);
return l;
}
相比维护BF,维护height更容易维护旋转后的高度,不用动脑无脑update就好了,多好啊!
在维护高度下,使用左右旋的条件是(伪代码):
if(Height(now->left)==Height(now->right)+2){
if(Height(now->left->left)>=Height(now->left->right)){
RotateRight(now);
}else{
RotateLeft(now->left);
RotateRight(now);
}
}else if(Height(now->right)==Height(now->left)+2){
if(Height(now->right->right)>=Height(now->right->left)){
RotateLeft(now);
}else{
RotateRight(now->right);
RotateLeft(now);
}
}
经过上述一轮旋转后,我们可以保证-1<=Height(l)-Height(r)<=1(证明略),即满足AVL树的条件。
插入
注意到,插入一个节点时,只有插入的节点路径上的height可能会变化。而且如果变化,一定是增加1。那么我们只要考虑某个子树插入(并有可能失衡进行旋转后)高度会不会变即可。考虑以root为根的子树,假如插入的节点位于root的左子树(右子树可以对称大法),那么考虑下面几种情况:
- 左子树增加了一个节点后没有长高,由
Height(root)=max(Height(l),Height(r))+1知高度不变。 - 左子树原来比右子树高,且左子树变高了,此时一定会失衡旋转,由旋转的性质知,高度不变(也是AVL平衡的基本原理)。
- 左子树比右子树矮,左子树变高了,由max知高度不变。
- 左子树和右子树一样高,左子树变高了,高度+1.
综上,如果higher(root)表示root为根的子树有没有变高,那么就有higher(root)=Height(l)==Height(r) && higher(l)。
这个递归可以轻松的转换成循环,理解其含义其实是从根到新加入的节点的路径上最后一个Height(l)!=Height(r)的地方开始高度+1.(特别的,如果不存在这样的地方,那么整棵树高度++):
AVL* blocker=NULL;
//find insert location
AVL* now=tree;
AVL* parent=NULL;
while(now!=NULL){
if(Height(now->left)!=Height(now->right)){
blocker=now;
}
if(data==now->value){
delete newNode;
return; //duplicate value in tree
}else if(data<now->value){
parent=now;
now=now->left;
}else if(data>now->value){
parent=now;
now=now->right;
}
}
if(data>parent->value){
parent->right=newNode;
}else{
parent->left=newNode;
}
//update height from blocker
now=blocker==NULL?tree:blocker;
while(now!=NULL){
if(data<now->value){
now=now->left;
}else if(data>now->value){
now=now->right;
}else{
break;
}
if(now!=NULL){
now->height++;
}
}
if(blocker==NULL){
//make sure total tree height is increased
tree->height++;
}
例如,按顺序插入3 2 1。插入2后:
3(H=2)
/
2(H=1)
此时插入1,blocker=3,我们只会更新节点1和2的高度:
3(H=2)
/
2(H=2)
/
1(H=1)
你会说,哎,不对啊?3的高度怎么错了,为什么不是3?对,我们上述算法所求的高度是假设已经旋转并平衡后的高度,现在我们树的结构还没有更新,所以高度看上去不对。对上面的树进行右旋1次,我们就会有:
2(H=2)
/ \
1(H1)3(H1)
这样树的高度就被正确反映出来了。
那么,算出了“真实”的高度后,我们怎么平衡呢?简单,只要沿着从根到新加节点的路径逐个查找左儿子真实高度和右儿子真实高度差距为2的点进行旋转就好了,让高度正确反映旋转后的状态。
要注意很多corner case,下面是平衡全部算法:
void balance(int data){
AVL* now=tree;
AVL* parent=NULL;
while(now!=NULL){
if(Height(now->left)==Height(now->right)+2){
if(Height(now->left->left)>=Height(now->left->right)){
if(parent==NULL){
tree=RotateRight(now);
}else{
if(parent->left==now){
parent->left=RotateRight(now);
}else{
parent->right=RotateRight(now);
}
}
}else{
now->left=RotateLeft(now->left);
if(parent==NULL){
tree=RotateRight(now);
}else{
if(parent->left==now){
parent->left=RotateRight(now);
}else{
parent->right=RotateRight(now);
}
}
}
}else if(Height(now->right)==Height(now->left)+2){
if(Height(now->right->right)>=Height(now->right->left)){
if(parent==NULL){
tree=RotateLeft(now);
}else{
if(parent->left==now){
parent->left=RotateLeft(now);
}else{
parent->right=RotateLeft(now);
}
}
}else{
now->right=RotateRight(now->right);
if(parent==NULL){
tree=RotateLeft(now);
}else{
if(parent->left==now){
parent->left=RotateLeft(now);
}else{
parent->right=RotateLeft(now);
}
}
}
}
if(now->value==data){
break;
}else if(data<now->value){
parent=now;
now=now->left;
}else{
parent=now;
now=now->right;
}
}
}
所以插入的过程就是:
- 找到插入位置,并插入节点
- 找到最后一个Height(l)!=Height(r)的节点,更新他子树下的高度
- 调准树的结构使其平衡
代码:
void Insert(int data){
AVL* newNode=new AVL();
newNode->height=0;
newNode->value=data;
if(tree==NULL){
newNode->height=1;
tree=newNode;
return;
}
AVL* blocker=NULL;
//find insert location
AVL* now=tree;
AVL* parent=NULL;
while(now!=NULL){
if(Height(now->left)!=Height(now->right)){
blocker=now;
}
if(data==now->value){
delete newNode;
return; //duplicate value in tree
}else if(data<now->value){
parent=now;
now=now->left;
}else if(data>now->value){
parent=now;
now=now->right;
}
}
if(data>parent->value){
parent->right=newNode;
}else{
parent->left=newNode;
}
//update height from blocker
now=blocker==NULL?tree:blocker;
while(now!=NULL){
if(data<now->value){
now=now->left;
}else if(data>now->value){
now=now->right;
}else{
break;
}
if(now!=NULL){
now->height++;
}
}
if(blocker==NULL){
//make sure total tree height is increased
tree->height++;
}
balance(data);
}
删除
AVL(BST)删除时,我们一定会先找到被删除节点的前驱(左子树最大值)或者后继(右子树最小值),用这个节点的值替换被删除节点原本的值,并形式上删除这个“替罪羊”节点,来保证BST的结构。本文采用删除前驱的方式。首先,我们就要找到形式上被删除的节点和要删除的节点:
AVL* now=tree;
AVL* parent=NULL;
AVL* thisNode=NULL;
AVL* toDelNode=NULL;
AVL* toDelPar=NULL;
//looking for the node holding value 'data'
while(now!=NULL){
if(now->value==data){
thisNode=now;
break;
}else if(data<now->value){
parent=now;
now=now->left;
}else{
parent=now;
now=now->right;
}
}
if(thisNode==NULL){
//not present in tree
return;
}
if(thisNode->left==NULL){
toDelPar=parent;
toDelNode=thisNode;
}else{
parent=thisNode;
now=thisNode->left;
while(now->right!=NULL){
parent=now;
now=now->right;
}
toDelPar=parent;
toDelNode=now;
}
接下来,和插入一样,我们注意到子树高度的改变一定发生在从根到toDelNode(形式上删除的节点)的路径中,且高度如果改变,一定是减少1。那么,考虑根root子树,假设删除的是左子树中的节点,高度什么时候会减少呢?考虑下列情况:
1. 删除后左子树高度没变,Height(root)不变。
2. 左子树高度比右子树高,左子树高度减少,Height(root)减少。
3. 左子树高度比右子树低,左子树高度减少,此时左子树高度比右子树低2,将会触发旋转。
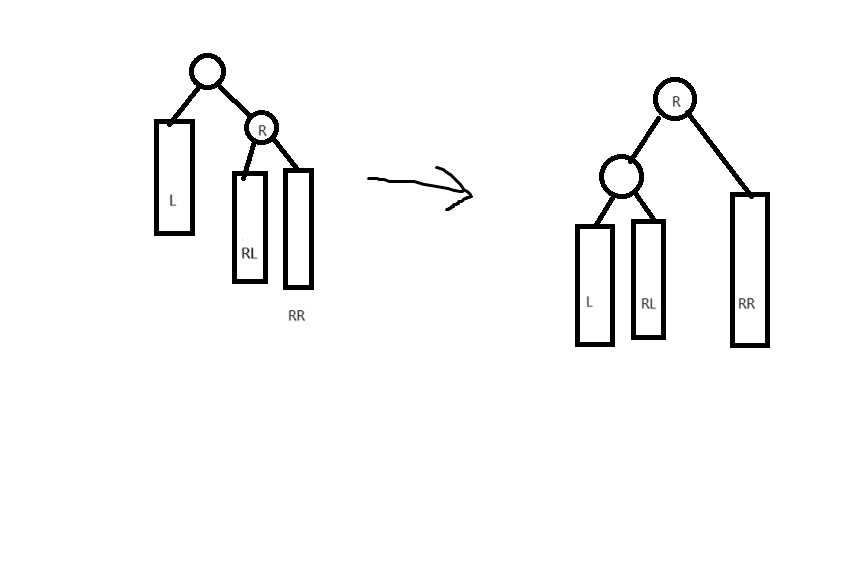
3.1. Height(rr)>=Height(rl),其中rr为右子树的右儿子,rl为右子树的左儿子,此时触发左单旋:
图中高度条件:Height(L)=Height(R)-2,Height(RR)=Height(RL)+1或Height(RR)=Height(RL)。
原高度:Height(RR)+2,旋转后高度:max(Height(RR)+1,Height(RL)+2),当且仅当Height(RR)>Height(RL)时高度变矮。
3.2. Height(rr)<Height(rl),此时触发左双旋:
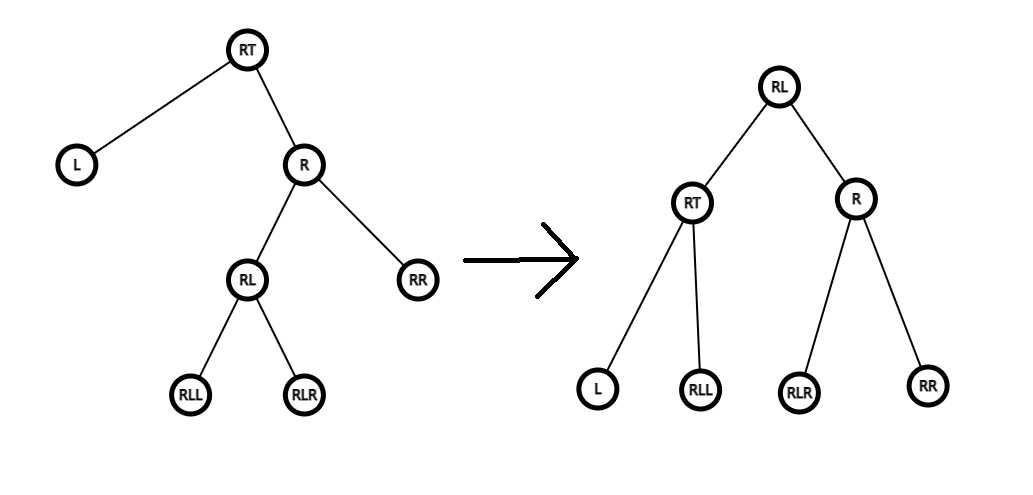
图中高度条件:Height(L)=Height(RL)-1,Height(RL)=Height(RR)+1
原高度:Height(RL)+2,现在高度:max(Height(L)+2,Height(RLL)+2,Height(RLR)+2,Height(RR)+2)。(这张图画的其实不好,没有体现出RLL、RLR,RR、L四个子树的大小关系,非常抱歉……)假设L的(修改完的)高度为h,那么R的高度是h+2(本来高度差是1,左边变矮了1格就变成了差2),RL的高度是h+1,RR的高度是h,RLL、RLR的高度是h/h-1(有一个一定是h)。那么这样来看,无论怎样高度都会变矮。
这一部分有点困难,希望您能自己在草稿纸上画张图搞清楚。
综上,shorter(root) = (Height(L)>Height(R) || Height(L)<Height(R) && Height(RL)!=Height(RR)) && shorter(L)
写成代码就是:
//find blocker
now=tree;
while(now!=NULL){
if(toDelNode->value==now->value){
break;
}
if(toDelNode->value<now->value){
if(!(Height(now->left)>Height(now->right) ||
Height(now->left)<Height(now->right) && Height(now->right->left)<Height(now->right->right) ||
Height(now->left)<Height(now->right) && Height(now->right->left)>Height(now->right->right) && Height(now->right->left->left)==Height(now->right->left->right))){
blocker=now;
}
now=now->left;
}else{
if(!(Height(now->right)>Height(now->left) ||
Height(now->right)<Height(now->left) && Height(now->left->right)!=Height(now->left->left))){
blocker=now;
}
now=now->right;
}
}
//start from blocker decrease height by 1
now=blocker==NULL?tree:blocker;
while(now!=NULL){
if(toDelNode->value==now->value){
break;
}else if(toDelNode->value<now->value){
now=now->left;
}else{
now=now->right;
}
if(now!=NULL){
now->height--;
}
}
if(blocker==NULL){
tree->height--;
}
当然,这一部分求出的高度也是 假设旋转、平衡后的高度,结构上还没更新。最后,我们在结构上删除并更新整棵树:
//actually removing toDelNode
bool needToCopy=toDelNode!=thisNode;
int valueDeleted=toDelNode->value;
AVL* toDelSubtree=toDelNode->left!=NULL?toDelNode->left:toDelNode->right;
if(toDelPar==NULL){
tree=toDelSubtree;
}else{
if(toDelNode==toDelPar->left){
toDelPar->left=toDelSubtree;
}else{
toDelPar->right=toDelSubtree;
}
}
delete toDelNode;
balance(valueDeleted);
//copy value to the original node
if(needToCopy){
thisNode->value=valueDeleted;
}
删除完整代码:
void Remove(int data){
if(tree==NULL){
return; //nothing to remove
}
AVL* now=tree;
AVL* parent=NULL;
AVL* thisNode=NULL;
AVL* toDelNode=NULL;
AVL* toDelPar=NULL;
AVL* blocker=NULL;
//looking for the node holding value 'data'
while(now!=NULL){
if(now->value==data){
thisNode=now;
break;
}else if(data<now->value){
parent=now;
now=now->left;
}else{
parent=now;
now=now->right;
}
}
if(thisNode==NULL){
//not present in tree
return;
}
if(thisNode->left==NULL){
toDelPar=parent;
toDelNode=thisNode;
}else{
parent=thisNode;
now=thisNode->left;
while(now->right!=NULL){
parent=now;
now=now->right;
}
toDelPar=parent;
toDelNode=now;
}
assert(toDelNode->left==NULL || toDelNode->right==NULL);
//find blocker
now=tree;
while(now!=NULL){
if(toDelNode->value==now->value){
break;
}
if(toDelNode->value<now->value){
if(!(Height(now->left)>Height(now->right) ||
Height(now->left)<Height(now->right) && Height(now->right->left)<Height(now->right->right) ||
Height(now->left)<Height(now->right) && Height(now->right->left)>Height(now->right->right) && Height(now->right->left->left)==Height(now->right->left->right))){
blocker=now;
}
now=now->left;
}else{
if(!(Height(now->right)>Height(now->left) ||
Height(now->right)<Height(now->left) && Height(now->left->right)<Height(now->left->left) ||
Height(now->right)<Height(now->left) && Height(now->left->right)>Height(now->left->left) && Height(now->left->right->left)==Height(now->left->right->right))){
blocker=now;
}
now=now->right;
}
}
//start from blocker decrease height by 1
now=blocker==NULL?tree:blocker;
while(now!=NULL){
if(toDelNode->value==now->value){
break;
}else if(toDelNode->value<now->value){
now=now->left;
}else{
now=now->right;
}
if(now!=NULL){
now->height--;
}
}
if(blocker==NULL){
tree->height--;
}
//actually removing toDelNode
bool needToCopy=toDelNode!=thisNode;
int valueDeleted=toDelNode->value;
AVL* toDelSubtree=toDelNode->left!=NULL?toDelNode->left:toDelNode->right;
if(toDelPar==NULL){
tree=toDelSubtree;
}else{
if(toDelNode==toDelPar->left){
toDelPar->left=toDelSubtree;
}else{
toDelPar->right=toDelSubtree;
}
}
delete toDelNode;
balance(valueDeleted);
if(needToCopy){
thisNode->value=valueDeleted;
}
}
完整代码
#include <bits/stdc++.h>
//#include "testlib.h"
using namespace std;
#define ll long long
#define pii pair<int,int>
#define qi ios::sync_with_stdio(0)
bool debug=true;
/* *************************************
* Written in Acer computer *
* The following code belongs to *
* XGN from HellHoleStudios *
*************************************
Current Problem Is:
*/
template<typename T1,typename T2>ostream& operator<<(ostream& os,pair<T1,T2> ptt){
os<<ptt.first<<","<<ptt.second;
return os;
}
template<typename T>ostream& operator<<(ostream& os,vector<T> vt){
os<<"{";
for(int i=0;i<vt.size();i++){
os<<vt[i]<<" ";
}
os<<"}";
return os;
}
struct AVL{
AVL* left;
AVL* right;
int value;
int height;
void print();
};
int Height(AVL* node){
return node==NULL? 0 : node->height;
}
void AVL::print(){
cout<<"(";
if(left!=NULL){
left->print();
}
cout<<value<<","<<Height(right)-Height(left);
if(right!=NULL){
right->print();
}
cout<<")";
}
void UpdateHeight(AVL* node){
node->height=max(Height(node->left),Height(node->right))+1;
}
//returns new root
AVL* RotateLeft(AVL* root){
AVL* r=root->right;
AVL* rl=root->right->left;
root->right=rl;
r->left=root;
UpdateHeight(root);
UpdateHeight(r);
return r;
}
//returns new root
AVL* RotateRight(AVL* root){
AVL* l=root->left;
AVL* lr=root->left->right;
l->right=root;
root->left=lr;
UpdateHeight(root);
UpdateHeight(l);
return l;
}
AVL* tree;
void balance(int data){
AVL* now=tree;
AVL* parent=NULL;
while(now!=NULL){
if(Height(now->left)==Height(now->right)+2){
if(Height(now->left->left)>=Height(now->left->right)){
if(parent==NULL){
tree=RotateRight(now);
}else{
if(parent->left==now){
parent->left=RotateRight(now);
}else{
parent->right=RotateRight(now);
}
}
}else{
now->left=RotateLeft(now->left);
if(parent==NULL){
tree=RotateRight(now);
}else{
if(parent->left==now){
parent->left=RotateRight(now);
}else{
parent->right=RotateRight(now);
}
}
}
}else if(Height(now->right)==Height(now->left)+2){
if(Height(now->right->right)>=Height(now->right->left)){
if(parent==NULL){
tree=RotateLeft(now);
}else{
if(parent->left==now){
parent->left=RotateLeft(now);
}else{
parent->right=RotateLeft(now);
}
}
}else{
now->right=RotateRight(now->right);
if(parent==NULL){
tree=RotateLeft(now);
}else{
if(parent->left==now){
parent->left=RotateLeft(now);
}else{
parent->right=RotateLeft(now);
}
}
}
}
if(now->value==data){
break;
}else if(data<now->value){
parent=now;
now=now->left;
}else{
parent=now;
now=now->right;
}
}
}
void Insert(int data){
AVL* newNode=new AVL();
newNode->height=0;
newNode->value=data;
if(tree==NULL){
newNode->height=1;
tree=newNode;
return;
}
AVL* blocker=NULL;
//find insert location
AVL* now=tree;
AVL* parent=NULL;
while(now!=NULL){
if(Height(now->left)!=Height(now->right)){
blocker=now;
}
if(data==now->value){
delete newNode;
return; //duplicate value in tree
}else if(data<now->value){
parent=now;
now=now->left;
}else if(data>now->value){
parent=now;
now=now->right;
}
}
if(data>parent->value){
parent->right=newNode;
}else{
parent->left=newNode;
}
//update height from blocker
now=blocker==NULL?tree:blocker;
while(now!=NULL){
if(data<now->value){
now=now->left;
}else if(data>now->value){
now=now->right;
}else{
break;
}
if(now!=NULL){
now->height++;
}
}
if(blocker==NULL){
//make sure total tree height is increased
tree->height++;
}
balance(data);
}
void Remove(int data){
// if(data==37){
// cout<<"Stop Here"<<endl;
// }
if(tree==NULL){
return; //nothing to remove
}
AVL* now=tree;
AVL* parent=NULL;
AVL* thisNode=NULL;
AVL* toDelNode=NULL;
AVL* toDelPar=NULL;
AVL* blocker=NULL;
//looking for the node holding value 'data'
while(now!=NULL){
if(now->value==data){
thisNode=now;
break;
}else if(data<now->value){
parent=now;
now=now->left;
}else{
parent=now;
now=now->right;
}
}
if(thisNode==NULL){
//not present in tree
return;
}
if(thisNode->left==NULL){
toDelPar=parent;
toDelNode=thisNode;
}else{
parent=thisNode;
now=thisNode->left;
while(now->right!=NULL){
parent=now;
now=now->right;
}
toDelPar=parent;
toDelNode=now;
}
assert(toDelNode->left==NULL || toDelNode->right==NULL);
//find blocker
now=tree;
while(now!=NULL){
if(toDelNode->value==now->value){
break;
}
if(toDelNode->value<now->value){
if(!(Height(now->left)>Height(now->right) ||
Height(now->left)<Height(now->right) && Height(now->right->left)!=Height(now->right->right))){
blocker=now;
}
now=now->left;
}else{
if(!(Height(now->right)>Height(now->left) ||
Height(now->right)<Height(now->left) && Height(now->left->right)!=Height(now->left->left))){
blocker=now;
}
now=now->right;
}
}
//start from blocker decrease height by 1
now=blocker==NULL?tree:blocker;
while(now!=NULL){
if(toDelNode->value==now->value){
break;
}else if(toDelNode->value<now->value){
now=now->left;
}else{
now=now->right;
}
if(now!=NULL){
now->height--;
}
}
if(blocker==NULL){
tree->height--;
}
//actually removing toDelNode
bool needToCopy=toDelNode!=thisNode;
int valueDeleted=toDelNode->value;
AVL* toDelSubtree=toDelNode->left!=NULL?toDelNode->left:toDelNode->right;
if(toDelPar==NULL){
tree=toDelSubtree;
}else{
if(toDelNode==toDelPar->left){
toDelPar->left=toDelSubtree;
}else{
toDelPar->right=toDelSubtree;
}
}
delete toDelNode;
balance(valueDeleted);
if(needToCopy){
thisNode->value=valueDeleted;
}
}
int main(int argc,char* argv[]){
// freopen("output/in.txt","r",stdin);
int n;
cin>>n;
for(int i=0;i<n;i++){
int op,data;
cin>>op>>data;
if(op==1){
Insert(data);
}else{
Remove(data);
}
tree->print();
cout<<endl;
}
return 0;
}
版权声明:
作者:XGN
链接:https://blog.hellholestudios.top/archives/1585
来源:Hell Hole Studios Blog
文章版权归作者所有,未经允许请勿转载。

共有 0 条评论